Introduction
Traditional reinforcement learning algorithms train an agent to solve a single task, expecting it to generalize well to unseen samples from a similar data distribution. Meta-learning trains a meta-learner on a distribution of similar tasks, in the hopes of generalization to novel but related tasks by learning a high-level strategy that captures the essence of the problem it is asked to solve.
Yan Duan et al. in 2016 structured a meta-learner, namely RL², as a recurrent neural network, which receives past rewards, actions, and termination flags as inputs in addition to the normally received observations. Despite its simplicity and universality, this approach is barely satisfactory in practice. Mishara et al. hypothesize that this is because traditional RNN architectures propagate information by keeping it in their hidden state from one timestep to the next; this temporally-linear dependency bottlenecks their capacity to perform sophisticated computation on a stream of inputs. Instead, they propose a Simple Neural AttentIve meta-Learner(SNAIL), which combines temporal convolutions and self-attention to distill useful information from the experience it gathers. This general-purposed model has shown its efficacy on a variety of experiments, including few-shot image classification and reinforcement learning tasks.
In this post, we will first introduce the structural components of SNAIL, specifically temporal convolutions and attention. Then we discuss their pros and cons and see how they complement each other. As usual, this post ends with a discussion.
Simple Neural Attentive Meta-Learner
The overall architecture of SNAIL goes first
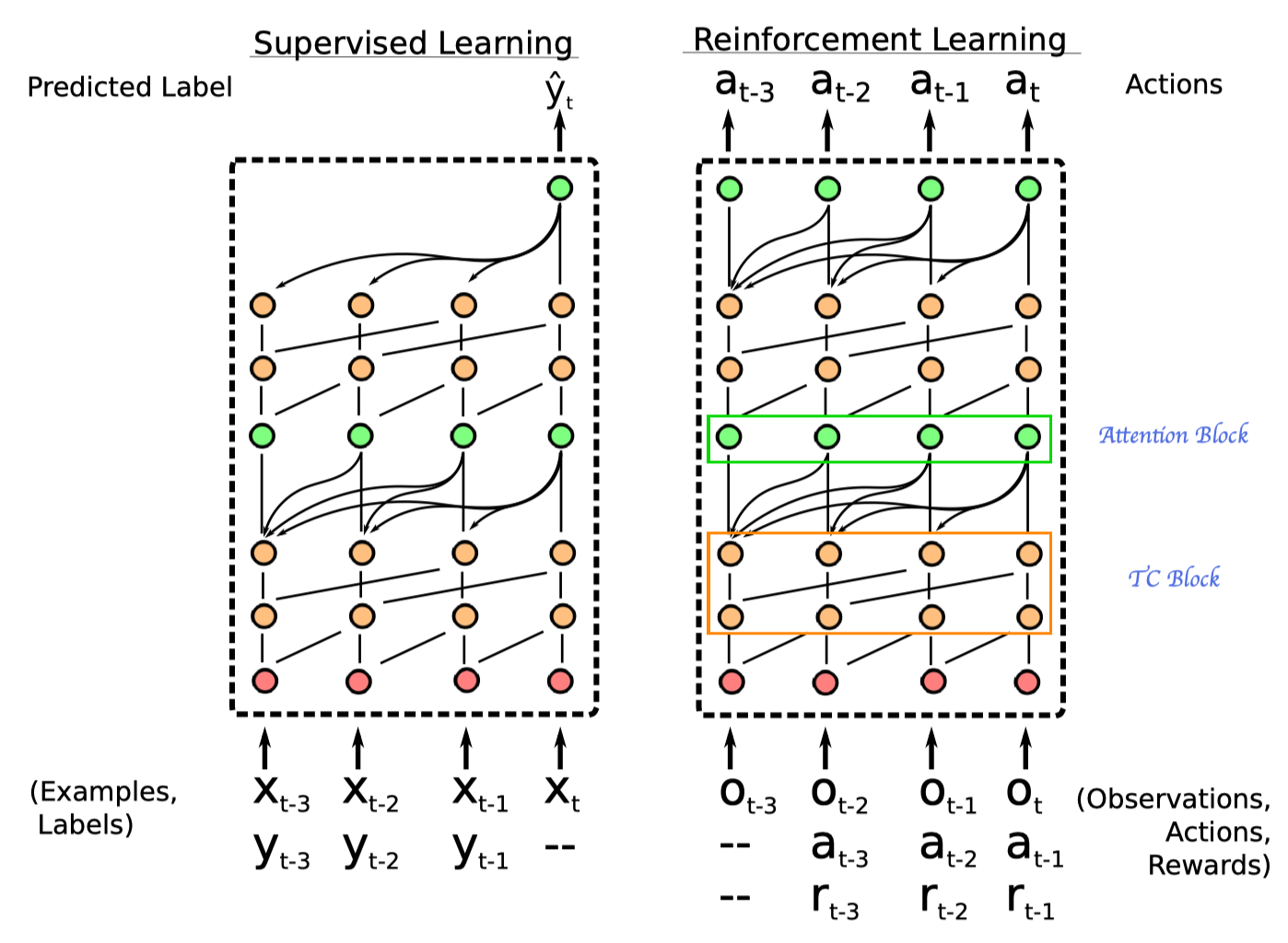
where green nodes represent attention block and orange nodes denote temporal convolution blocks. Now let us take a deeper look at each component.
Temporal Convolutions
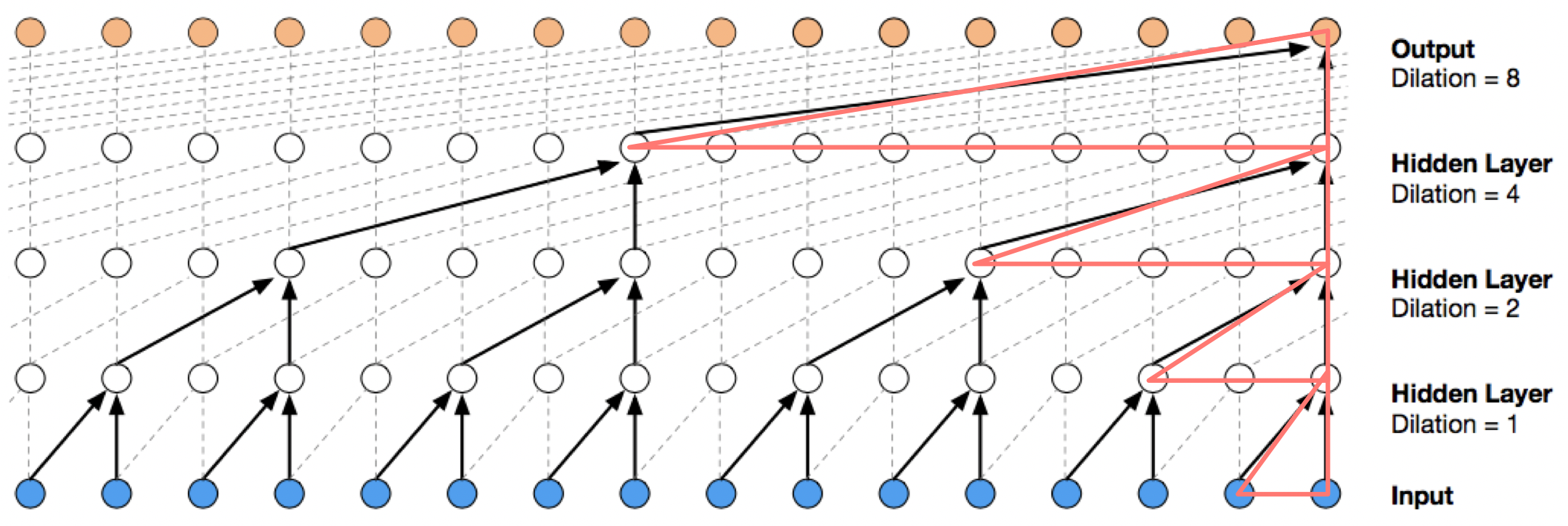
Before discussing the structure of temporal convolutions(TC), we first introduce a dense block, which applies a single causal 1D-convolution with kernel size 2, dilation rate \(R\) and \(D\)(e.g., \(16\)) filters, and then concatenates the result with its input.
\[\begin{align} &1.\quad\mathbf{Func}\ \mathrm{DenseBlock}(x, R, D):\\\ &2.\quad\quad x_f, x_g=\mathrm{CausalConv}(x, R, D), \mathrm{CausalConv}(x,R,D)\\\ &3.\quad\quad y=\tanh(x_f)*\sigma(x_g)\\\ &4.\quad\quad \mathbf{return}\ \mathrm{concat}(x,y) \end{align}\]Causal 1D-convolution filters are illustrated by the red triangles in Figure 2, with dilation rates \(8, 4, 2, 1\) from the top down. Note that 1D-convolution is applied to the sequence dimension, and the data dimension is treated as the channel dimension. The causal convolution helps summarize temporal information just as 2-D convolutions summarize spatial information. In the 3rd line we use the gated activation function, which has been wildly used in LSTM and GRUs.
A TC block consists of a series of dense blocks whose dilation rates increase exponentially until their receptive filed exceeds the desired sequence length \(T\) so that nodes in the last layer captures all past information.
\[\begin{align} &1.\quad\mathbf{Func}\ \mathrm{TCBlock}(x, T, D):\\\ &2.\quad\quad \mathbf{for}\ i\ \mathrm{in}\ 1,\dots,\ \lceil\log_2T\rceil\ \mathbf{do}\\\ &3.\quad\quad\quad x=\mathrm{DenseBlock}(x, 2^{i-1}, D)\\\ &4.\quad\quad\mathbf{return\ }x \end{align}\]Attention
An attention block performs a key-value lookup; we style this operation after the scaled dot-product attention, which has been covered in the previous post:
\[\begin{align} &1.\quad\mathbf{Func}\ \mathrm{AttentionBlock}(x, d_K, d_V)\\\ &2.\quad\quad K, Q=\mathrm{fc}(x,d_K), \mathrm{fc}(x,d_K)\\\ &3.\quad\quad logits=QK^T\\\ &4.\quad\quad P=\mathrm{CausallyMaskedSoftmax}(logits/\sqrt{d_K})\\\ &5.\quad\quad V=\mathrm{fc}(x,d_V)\\\ &6.\quad\quad y=PV\\\ &7.\quad\quad \mathbf{return}\ \mathrm{concat}(x,y) \end{align}\]where \(d_K\), \(d_V\) are the dimensions of the key and value, respectively. In their experiments, both \(d_K\) and \(d_V\) are set to be \(16\) or \(32\). The causal mask is essentially important here, since otherwise the attention block could suffer from data leakage, where future data are leaked to the current time step.
Cooperation between Temporal Convolutions and Attention
Thanks to dilated causal convolutions, which supports exponentially expanding receptive fields without losing resolution or coverage, temporal convolutions offer more direct, high-bandwidth access to past information, compared to traditional RNNs. This allows them to perform more sophisticated computation over a temporal context of fixed size. However, to scale to long sequences, the dilation rates generally increase exponentially, so that the required number of layers scales logarithmically with the sequence length. Their bounded capacity and positional dependence can be undesirable in a meta-learner, which should be able to fully utilize increasingly large amounts of experience.
In contrast, soft attention allows a model to pinpoint a specific piece of information, from a potentially infinitely-large context. However, the lack of positional dependence can also be undesirable, especially in reinforcement learning, where the observations, actions, and rewards are intrinsically sequential.
Despite their individual shortcomings, temporal convolutions and attentions complement each other: while the former provides high-bandwidth access at the expense of finite context size, the latter provide pinpoint access over an infinitely large context. By interleaving TC layers with causal attention layers, SNAIL can have high-bandwidth access over its past experience without constraints on the amount of experience it can effectively use. By using attention at multiple stages within a model that is trained end-to-end, SNAIL can learn what pieces of information to pick out from the experience it gathers, as well as a feature representation that is amenable to doing so easily. In short, temporal convolutions learn how to aggregate contextual information, from which attention learns how to distill specific piece of information.
Discussion
How is SNAIL trained?
It is trained in almost the same way that on-policy algorithms with RNNs are trained except that we use an entire episode in a minibatch here.
How does SNAIL make a decision?
I perfonally think that SNAIL makes decisions using a minibatch of size \(T\), which includes the current observation in addition to observation-action pairs from the previous episode. What I do not understand is that the authors claim SNAIL maintains the internal state:
Crucially, following existing work in meta-RL (Duan et al., 2016; Wang et al., 2016), we preserve the internal state of a SNAIL across episode boundaries, which allows it to have memory that spans multiple episodes. The observations also contain a binary input that indicates episode termination.
Welcome to discuss this on StackOverflow
References
Yan Duan et al. RL\(^2\) : Fast Reinforcement Learning via Slow Reinforcement Learning
Fisher Yu et al. Multi-Scale Context Aggregation by Dilated Convolutions
Nikhil Mishra et al. A Simple Neural Attentive Meta-Learner
Ashish Vaswani et al. Attention Is All You Need


